Diet Plan To Reduce 10 Kg In 15 Days

Empty Message

Finding The Area Of A Sector Of A Circle Calculator

In geometry, circle sector is a part of a circle lying between two straight lines drawn from the centre to the edge. The formula, solved example & step by step calculations may useful for users to understand how the input values are being used in such sector area calculations. Also this featured sector area calculator uses the various conversion functions to find its volume in SI or metric or US customary units. Circles are everywhere in the real world, which is why their radii, diameters and circumference are significant in real life applications. But there are other parts of circles – sectors and angles, for instance – that also have importance in everyday applications as well. For these reasons and more, geometry also has equations and problem calculations dealing with central angles, arcs and sectors of a circle.

Sometimes you might need to determine the area of a sector, say for math questions or for a project you are working on. A sector is a part of a circle that is shaped like a piece of pizza or pie. To find the area of this piece, you need to know the radius, arc length and the degree of the central angle.

With this information, finding the area of a sector is a simple matter of plugging the numbers into given formulas. The central angle is defined as the angle created by two rays or radii radiating from the center of a circle, with the circle's center being the vertex of the central angle. Central angles are particularly relevant when it comes to evenly dividing up pizza, or any other circular-based food, among a set number of people.

Say there are five people at a soiree where a large pizza and a large cake are to be shared. What is the angle that both the pizza and the cake have to be divided at to ensure an equal slice for everyone? Unlike triangles, the boundaries of sectors are not established by line segments. The distance along that curved "side" is the arc length.

You will instantly get the area of sector with the step by step demonstration of the calculation. It also shows the formula that it used to find the sector of circle. Sector area calculator only finds the inner portion of circle. If you want to calculate the circumference of circle, you can use ourcircumference calculatoranytime.

In the field of area & volume calculations, finding the sector area of a circle is important to understand basic mathematical computations. The following mathematical formula is used in this circular sector calculator to find the area for the given input values of radius r & the angle θ in degrees. Radian is the angle formed when the radius and the sector of the circle is covered, just like placing the compass at the center point and moving over the circumference of the circle.

Use this simple Area of a Segment of a Circle Calculator based on Radius and Radians to find the segment area circle. This can be calculated by first finding the area of the particular sector of circle and subtracting the area of the triangle formed by the given radian and radius. Angles are measured in degrees, but sometimes to make the mathematics simpler and elegant it's better to use radians which is another way of denoting an angle.

A radian is the angle subtended by an arc of length equal to the radius of the circle. ( "Subtended" means produced by joining two lines from the end points of the arc to the center). The measure of the central angle or the length of the arc. The central angle is the angle subtended by an arc of a sector at the center of a circle. The central angle can be given in degrees or radians.

Anytime you cut a slice out of a pumpkin pie, a round birthday cake, or a circular pizza, you are removing a sector. A sector is created by the central angle formed with two radii, and it includes the area inside the circle from that center point to the circle itself. The portion of the circle's circumference bounded by the radii, the arc, is part of the sector.

Circumference of a circle calculator works according to the above-given formula. You can find the circumference calculator useful to solve circumference online. Also try our cbm calculator to calculate triangles, cubic feet from length and width.

There are two types of sectors, minor and major sector. A minor sector is less than a semi-circle sector, whereas a major sector is a sector that is greater than a semi-circle. Getcalc.com's circle sector calculator is an online basic geometry tool to calculate area of sector & length of an arc , in both US customary & metric units. You can use circumference formula calculator to solve circumference online. For manual calculations, let's assume we draw a circle of radius 3.5 centimeters. As we know this blue boundary of the circle will be its perimeter.

The perimeter of the circle is also called circumference. You can use this calculator for the perimeter of a sector based on sector angle and radius. You can also calculate sector arc length and sector area using this tool. But the formula for the perimeter of a sector is not that straightforward.

The sector is a part of a circle or you may call it a slice as you see in a pizza. The perimeter of a sector in a circle is dependent on the angle that it makes at the center. The perimeter of a sector is called the circumference of the sector. In this article, we discuss the formula for the perimeter of a sector in a circle. Find the area, correct to two decimal places, of the minor segment in a circle of radius 10 cm where the angle subtended at the centre of the circle by the chord is $$. © Eugene BrennanThis guide explains everything you need to know about circles, including calculation of area, segment area, sector area, length of an arc, radians, sine and cosine.

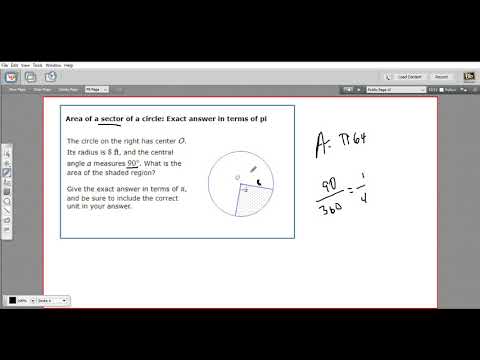
To calculate the area of a sector, start by finding the central angle of the sector and dividing it by 360. Next, take the radius, or length of one of the lines, square it, and multiply it by 3.14. Then, multiply the two numbers to get the area of the sector. For example, if the central angle is 100 degrees and the radius is 5, you would divide 100 by 360 to get .28. Then, square 5 to get 25 before multiplying it by 3.14 for an answer of 78.5.

Finally, multiply .28 by 78.5 for a final answer of 21.89, which is the area of the sector. For example, if you know the sector is one-fourth of the circle, multiply 360 by one-fourth (.25) to get 90 degrees. The following table gives the formulas for the area of sector and area of segment for angles in degrees or radians. Scroll down the page for more explanations, examples and worksheets for the area of sectors and segments.

The area of a sector of a circle is the amount of space enclosed within the boundary of the sector. A sector always originates from the center of the circle. The sector of a circle is defined as the portion of a circle that is enclosed between its two radii and the arc adjoining them. The semi-circle is the most common sector of a circle, which represents half a circle. Let us learn more about the area of sector, its formula, and how to calculate the area of a sector using radians and degrees. An online area of a sector calculator is specifically programmed to find the area of the sector, the arc length, and chord length of a circle sector.

This free calculator generates accurate outputs so you may not feel any difficulty during your calculations. But before we move further, let us make sure that you need to memorize some crucial terms which are as follows. If they tell you that the area of a 60 degree sector is 14 square cm., think about what fraction of the "whole pie" this "slice" is.

Area Of A Sector Of A Circle Formula Calculator A circle is a 360 degree arc, so 60 degrees is (60/360) or (1/6) of a whole circle. You would have to multiply the sector area by 6 to get the area of the whole circle. Acute central angles will always produce minor arcs and small sectors. When the central angle formed by the two radii is 90°, the sector is called a quadrant . When the two radii form a 180°, or half the circle, the sector is called a semicircle and has a major arc. The area of a sector along an arc is also known as the circular sector.

It's a percent or portion of a disk that is enclosed by that arc and two equal radii. To understand how to calculate the area of such a sector, it's important to understand the formula that it uses, which is given above. Divide the length of the arc by the length of the circumference. That gives you the fraction of the circumference represented by the arc.

Plug the sector's central angle measurement into the formula. Doing this will give you what fraction or percent of the entire circle the sector represents. We can calculate the area of the sector, given the central angle and radius of circle. K-12 students may refer the below formulas of circle sector to know what are all the input parameters are being used to find the area and arc length of a circle sector. The step by step workout for how to find what is area & length of a circle sector.

Students may use this circle sector calculator to generate work with steps for any other similar input values. To calculate the Area of Sector, Area of sector of Circle given central angle and radius is part of the disk, which is bounded by two radii and an arc between the radii. Thus, a sector's area is equal to the radius r squared times the central angle θ in radians, divided by 2. Calculate the area of a sector using the central angle and radius below and learn the formula and steps to solve it below. Please input radius of the circle and the central angle in degrees, then click Calculate Area of Sector button. The calculator will show you the chart of the sector based on your input as well.

The area of a circle is any space that the circle occupies on a flat surface. When we talk about the surface area of the circle, we are focusing on two-dimensional objects. When finding the circle area, there are three other measures that we take into consideration, including the circumference, diameter, and radius. All three calculations also help us fining the circle area.

The angle at center of arc is degrees and radius of circle is . A sector is said to be a part of a circle made of the arc of the circle along with its two radii. It is a portion of the circle formed by a portion of the circumference and radii of the circle at both endpoints of the arc. The shape of a sector of a circle can be compared with a slice of pizza or a pie. Before we start learning more about the sector, first let us learn some basics of the circle.

This tool can be used to solve geometry problems related tocircle. Moreover, it can be used to measure the land in sectors, and some cool things such slice of pizza or cake. A circle is 360 degrees, so when you place the measurement of the sector's central angle over 360, it gives you the fraction of the whole circle. Let us use these formulas and learn how to calculate the area of the sector of a circle when the subtended angle is given in degrees with the help of an example. Let us apply the unitary method to derive the formula for the area of the sector of a circle. The area of a circle with an angle measuring 360º at the center is given by πr2, where 'r' is the radius of the circle.

To calculate Area of sector of Circle given central angle and radius, you need Radius & Central Angle . With our tool, you need to enter the respective value for Radius & Central Angle and hit the calculate button. You can also select the units for Input and the Output as well.

Only a mathematician can genuinely understand the practical importance of formulas for calculating area, radius, diameter, or circle circumference. While most people think that formulas have no practical use, they are critical factors in many everyday life routines. If the area of the circle is not equal to that of the triangle, then it must be either greater or less. We eliminate each of these by contradiction, leaving equality as the only possibility. If, instead of a central angle in degrees, you are given the radians, you use an even easier formula. Once you know the radius, you have the lengths of two of the parts of the sector.

You only need to know arc length or the central angle, in degrees or radians. Use our online calculator to perform area of a sector of a circle calculation. To calculate the area of the sector you must first calculate the area of the equivalent circle using the formula stated previously. Then, you must multiply that area by the ratio of the angles which would be theta/360 since the circle is 360, and theta is the angle of the sector. Calculate the area of a sector using the radius of an arc and the angle of rotation. This area uses units of degrees for the angle and any unit of distance for the radius.

Next, we will look at the formula for the area of a sector where the central angle is measured in radians. Recall that the angle of a full circle in radians is 2π. We can calculate the central angle subtended by a sector, given the area of the sector and area of circle. Comparing the area of sector and area of circle, we derive the formula for the area of sector when the central angle is given in degrees. We will now look at the formula for the area of a sector where the central angle is measured in degrees. Circumference formula calculator is simple and very easy to use.

To calculate the circumference of a circle, just provide radius to our circumference calculator and get your answer. Our circumference to diameter calculator will show you diameter, circumference & area as the results. To avoid manual calculations one can use circumference formula calculator to get equation for circumference solved quickly, For manual calculations, process is below mentioned. Here if you ever get stuck during calculations of these quantities, try using the free online area of a sector calculator.

You will always get accurate answers regarding each term that you wish to find. You may, very rarely, hear about the sector of an ellipse, but the formulas are way, way more difficult to use than the circle sector area equations. Finding the radius is not always easy, especially if you don't have the circle's center. You can calculate the area using the diameter instead. The same formula applies as above, but you need first to calculate the radius of the circle. Simply divide the diameter by 2 to get the radius.